Понятие о статистической достоверности. Уровень статистической достоверности
Рассмотрим типичный пример применения статистических методов в медицине. Создатели препарата предполагают, что он увеличивает диурез пропорционально принятой дозе. Для проверки этого предположения они назначают пяти добровольцам разные дозы препарата.
По результатам наблюдений строят график зависимости диуреза от дозы (рис. 1.2А). Зависимость видна невооруженным глазом. Исследователи поздравляют друг друга с открытием, а мир - с новым диуретиком.
На самом деле данные позволяют достоверно утверждать лишь то, что зависимость диуреза от дозы наблюдалась у этих пяти добровольцев. То, что эта зависимость проявится у всех людей, которые будут принимать препарат, - не более чем предполо-
зЯ

 с
с
жение. Нельзя сказать, что оно беспочвенно - иначе, зачем ставить эксперименты?
Но вот препарат поступил в продажу. Все больше людей принимают его в надежде увеличить свой диурез. И что же мы видим? Мы видим рис 1.2Б, который свидетельствует об отсутствии какой либо связи между дозой препарата и диурезом. Черными кружками отмечены данные первоначального исследования. Статистика располагает методами, позволяющими оценить вероятность получения столь «непредставительной», более того, сбивающей с толку выборки. Оказывается в отсутствие связи между диурезом и дозой препарата полученная «зависимость» наблюдалась бы примерно в 5 из 1000 экспериментов. Итак, в данном случае исследователям просто не повезло. Если бы они применили даже самые совершенные статистические методы, это все равно не спасло бы их от ошибки.
Этот вымышленный, но совсем не далекий от реальности пример, мы привели не для того, чтобы указать на бесполез
ность статистики. Он говорит о другом, о вероятностном характере ее выводов. В результате применения статистического метода мы получаем не истину в последней инстанции, а всего лишь оценку вероятности того или иного предположения. Кроме того, каждый статистический метод основан на собственной математической модели и результаты его правильны настолько насколько эта модель соответствует действительности.
Еще по теме ДОСТОВЕРНОСТЬ И СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ:
- Статистически значимые отличия показателей качества жизни
- Статистическая совокупность. Учетные признаки. Понятие о сплошных и выборочных исследованиях. Требования к статистической совокупности и использованию учетно-отчетных документов
- РЕФЕРАТ. ИССЛЕДОВАНИЕ ДОСТОВЕРНОСТИ ПОКАЗАНИЙ ТОНОМЕТРА ДЛЯ ИЗМЕРЕНИЯ ВНУТРИГЛАЗНОГО ДАВЛЕНИЯ ЧЕРЕЗ ВЕКО2018, 2018
Если действовать не будешь, ни к чему ума палата. (Шота Руставели)
Основные термины и понятия медицинской статистики
В данной статье мы приведем некоторые ключевые понятия статистики, актуальные при проведении медицинских исследований. Более подробно термины разбираются в соответствующих статьях.
Вариация
Определение. Степень рассеяния данных (значений признака) по области значений
Вероятность
Определение . Вероятность(probability) - степень возможности проявления какого - либо определённого события в тех или иных условиях.
Пример. Поясним определение термина на предложении «Вероятность выздоровления при применении лекарственного препарата Aримидекс равна 70%». Событием является «выздоровление больного», условием «больной принимает Аримидекс», степенью возможности - 70% (грубо говоря, из 100 человек, принимающих Аримидекс, выздоравливают 70).
Кумулятивная вероятность
Определение. Кумулятивная вероятность выживания (Cumulative Probability of surviving) в момент времени t - это то же самое, что доля выживших пациентов к этому моменту времени.
Пример. Если говорится, что кумулятивная вероятность выживания после проведения пятилетнего курса лечения равна 0.7, то это значит, что из рассматриваемой группы пациентов в живых осталось 70% от начального количества, а 30% умерло. Другими словами, из каждой сотни человек 30 умерло в течение первых 5 лет.
Время до события
Определение. Время до события - это время, выраженное в некоторых единицах, прошедшее с некоторого начального момента времени до наступления некоторого события.
Пояснение. В качестве единиц времени в медицинских исследованиях выступают дни, месяцы и годы.
Типичные примеры начальных моментов времени:
начало наблюдения за пациентом
проведение хирургического лечения
Типичные примеры рассматриваемых событий:
прогрессирование болезни
возникновение рецидива
смерть пациента
Выборка
Определение. Часть популяции, полученная путем отбора.
По результатам анализа выборки делают выводы о всей популяции, что правомерно только в случае, если отбор был случайным. Поскольку случайный отбор из популяции осуществить практически невозможно, следует стремиться к тому, чтобы выборка была по крайней мере репрезентативна по отношению к популяции.
Зависимые и независимые выборки
Определение. Выборки, в которые объекты исследования набирались независимо друг от друга. Альтернатива независимым выборкам - зависимые (связные, парные) выборки.
Гипотеза
Двусторонняя и односторонняя гипотезы
Сначала поясним применение термина гипотеза в статистике.
Цель большинства исследований - проверка истинности некоторого утверждения. Целью тестирования лекарственных препараторов чаще всего является проверка гипотезы, что одно лекарство эффективнее другого (например, Аримидекс эффективнее Тамоксифена).
Для предания строгости исследования, проверяемое утверждение выражают математически. Например, если А - это количество лет, которое проживёт пациент, принимающий Аримидекс, а Т -это количество лет, которое проживёт пациент, принимающий Тамоксифен, то проверяемую гипотезу можно записать как А>Т.
Определение. Гипотеза называется двусторонней (2-sided), если она состоит в равенстве двух величин.
Пример двусторонней гипотезы: A=T.
Определение. Гипотеза называется односторонней (1-sided),если она состоит в неравенстве двух величин.
Примеры односторонних гипотез:
Дихотомические (бинарные) данные
Определение. Данные, выражаемые только двумя допустимыми альтернативными значениями
Пример: Пациент «здоров» - «болен». Отек "есть" - "нет".
Доверительный интервал
Определение. Доверительный интервал (confidence interval) для некоторой величины - это диапазон вокруг значения величины, в котором находится истинное значение этой величины (с определенным уровнем доверия).
Пример. Пусть исследуемой величиной является количество пациентов в год. В среднем их количество равно 500, а 95% -доверительный интервал - (350, 900). Это означает, что, скорее всего (с вероятностью 95%), в течение года в клинику обратятся не менее 350 и не более 900 человек.
Обозначение. Очень часто используются сокращение: ДИ 95 % (CI 95%) - это доверительный интервал с уровнем доверия 95%.
Достоверность, статистическая значимость (P - уровень)
Определение. Статистическая значимость результата - это мера уверенности в его "истинности".
Любое исследование проходит на основе лишь части объектов. Исследование эффективности лекарственного препарата проводится на основе не вообще всех больных на планете, а лишь некоторой группы пациентов (провести анализ на основе всех больных просто невозможно).
Предположим, что в результате анализа был сделан некоторый вывод (например, использование в качестве адекватной терапии препарата Аримидекс в 2 раза эффективнее, чем препарата Тамоксифен).
Вопрос, который необходимо при этом задавать: "Насколько можно доверять этому результату?".
Представьте, что мы проводили исследование на основе только двух пациентов. Конечно же, в этом случае к результатам нужно относиться с опасением. Если же были обследовано большое количество больных (численное значение «большого количества» зависит от ситуации), то сделанным выводам уже можно доверять.
Так вот, степень доверия и определяется значением p-уровня (p-value).
Более высокий p- уровень соответствует более низкому уровню доверия к результатам, полученным при анализе выборки. Например, p- уровень, равный 0.05 (5%) показывает, что сделанный при анализе некоторой группы вывод является лишь случайной особенностью этих объектов с вероятностью только 5%.
Другими словами, с очень большой вероятностью (95%) вывод можно распространить на все объекты.
Во многих исследованиях 5% рассматривается как приемлемое значение p-уровня. Это значит, что если, например, p= 0.01, то результатам доверять можно, а если p=0.06, то нельзя.
Исследование
Проспективное исследование - это исследование, в котором выборки выделяются на основе исходного фактора, а в выборках анализируется некоторый результирующий фактор.
Ретроспективное исследование - это исследование, в котором выборки выделяются на основе результирующего фактора, а в выборках анализируется некоторый исходный фактор.
Пример. Исходный фактор - беременная женщина моложе/старше 20 лет. Результирующий фактор - ребёнок легче/тяжелее 2,5 кг. Анализируем, зависит ли вес ребёнка от возраста матери.
Если мы набираем 2 выборки, в одной - матери моложе 20 лет, в другой - старше, а затем анализируем массу детей в каждой группе, то это проспективное исследование.
Если мы набираем 2 выборки, в одной - матери, родившие детей легче 2,5 кг, в другой - тяжелее, а затем анализируем возраст матерей в каждой группе, то это ретроспективное исследование (естественно, такое исследование можно провести, только когда опыт закончен, т.е. все дети родились).
Исход
Определение. Клинически значимое явление, лабораторный показатель или признак, который служит объектом интереса исследователя. При проведении клинических испытаний исходы служат критериями оценки эффективности лечебного или профилактического воздействия.
Клиническая эпидемиология
Определение. Наука, позволяющая осуществлять прогнозирование того или иного исхода для каждого конкретного больного на основании изучения клинического течения болезни в аналогичных случаях с использованием строгих научных методов изучения больных для обеспечения точности прогнозов.
Когорта
Определение. Группа участников исследования, объединенных каким-либо общим признаком в момент ее формирования и исследуемых на протяжении длительного периода времени.
Контроль
Контроль исторический
Определение. Контрольная группа, сформированная и обследованная в период, предшествующий исследованию.
Контроль параллельный
Определение. Контрольная группа, формируемая одновременно с формированием основной группы.
Корреляция
Определение. Статистическая связь двух признаков (количественных или порядковых), показывающая, что большему значению одного признака в определенной части случаев соответствует большее - в случае положительной (прямой) корреляции - значение другого признака или меньшее значение - в случае отрицательной (обратной) корреляции.
Пример. Между уровнем тромбоцитов и лейкоцитов в крови пациента обнаружена значимая корреляция. Коэффициент корреляции равен 0,76.
Коэффициент риска (КР)
Определение. Коэффициент риска (hazard ratio) - это отношение вероятности наступления некоторого («нехорошего») события для первой группы объектов к вероятности наступления этого же события для второй группы объектов.
Пример. Если вероятность появления рака лёгких у некурящих равна 20%, а у курильщиков - 100%, то КР будет равен одной пятой. В этом примере первой группой объектов являются некурящие люди, второй группой - курящие, а в качестве «нехорошего» события рассматривается возникновение рака лёгких.
Очевидно, что:
1) если КР=1, то вероятность наступления события в группах одинаковая
2) если КР>1, то событие чаще происходит с объектами из первой группы, чем из второй
3) если КР<1, то событие чаще происходит с объектами из второй группы, чем из первой
Мета-анализ
Определение. С
татистический анализ, обобщающий результаты нескольких исследований, исследующих одну и ту же проблему (обычно эффективность методов лечения, профилактики, диагностики). Объединение исследований обеспечивает большую выборку для анализа и большую статистическую мощность объединяемых исследований. Используется для повышения доказательности или уверенности в заключении об эффективности исследуемого метода.
Метод Каплана - Мейера (Множительные оценки Каплана - Мейера)
Этот метод был придуман статистиками Е.Л.Капланом и Полем Мейером.
Метод используется для вычисления различных величин, связанных с временем наблюдения за пациентом. Примеры таких величин:
вероятность выздоровления в течении одного года при применении лекарственного препарата
шанс возникновения рецидива после операции в течении трёх лет после операции
кумулятивная вероятность выживания в течение пяти лет среди пациентов с раком простаты при ампутации органа
Поясним преимущества использования метода Каплана - Мейера.
Значение величин при «обычном» анализе (не использующем метод Каплана-Мейера) рассчитываются на основе разбиения рассматриваемого временного интервала на промежутки.
Например, если мы исследуем вероятность смерти пациента в течение 5 лет, то временной интервал может быть разделён как на 5 частей (менее 1 года, 1-2 года, 2-3 года, 3-4 года, 4-5 лет), так и на 10 (по полгода каждый), или на другое количество интервалов. Результаты же при разных разбиениях получатся разные.
Выбор наиболее подходящего разбиения - непростая задача.
Оценки значений величин, полученных по методу Каплана- Мейера не зависят от разбиения времени наблюдения на интервалы, а зависят только от времени жизни каждого отдельного пациента.
Поэтому исследователю проще проводить анализ, да и результаты нередко оказываются качественней результатов «обычного» анализа.
Кривая Каплана -Мейера (Kaplan - Meier curve)- это график кривой выживаемости, полученной по методу Каплана-Мейера.
Модель Кокса
Эта модель была придумана сэром Дэвидом Роксби Коксом (р.1924), известным английским статистиком, автором более 300 статей и книг.
Модель Кокса используется в ситуациях, когда исследуемые при анализе выживаемости величины зависят от функций времени. Например, вероятность возникновения рецидива через t лет (t=1,2,…), может зависеть от логарифма времени log(t).
Важным достоинством метода, предложенного Коксом, является применимость этого метода в большом количестве ситуаций (модель не накладывает жестких ограничений на природу или форму распределения вероятностей).
На основе модели Кокса можно проводить анализ (называемый анализом Кокса (Cox analysis)), результатом проведения которого является значение коэффициента риска и доверительного интервала для коэффициента риска.
Непараметрические методы статистики
Определение. Класс статистических методов, которые используются главным образом для анализа количественных данных, не образующих нормальное распределение, а также для анализа качественных данных.
Пример. Для выявления значимости различий систолического давления пациентов в зависимости от типа лечения воспользуемся непараметрическим критерием Манна-Уитни.
Признак (переменная)
Определение. Х арактеристика объекта исследования (наблюдения). Различают качественные и количественные признаки.
Рандомизация
Определение. Способ случайного распределения объектов исследования в основную и контрольную группы с использованием специальных средств (таблиц или счетчика случайных чисел, подбрасывания монеты и других способов случайного назначения номера группы включаемому наблюдению). С помощью рандомизации сводятся к минимуму различия между группами по известным и неизвестным признакам, потенциально влияющим на изучаемый исход.
Риск
Атрибутивный - дополнительный риск возникновения неблагоприятного исхода (например, заболевания) в связи с наличием определенной характеристики (фактора риска) у объекта исследования. Это часть риска развития болезни, которая связана с данным фактором риска, объясняется им и может быть устранена, если этот фактор риска устранить.
Относительный риск - отношение риска возникновения неблагоприятного состояния в одной группе к риску этого состояния в другой группе. Используется в проспективных и наблюдательных исследованиях, когда группы формируются заранее, а возникновение исследуемого состояния ещё не произошло.
Скользящий экзамен
Определение. Метод проверки устойчивости, надежности, работоспособности (валидности) статистической модели путем поочередного удаления наблюдений и пересчета модели. Чем более сходны полученные модели, тем более устойчива, надежна модель.
Событие
Определение. Клинический исход, наблюдаемый в исследовании, например возникновение осложнения, рецидива, наступление выздоровления, смерти.
Стратификация
Определение. М етод формирования выборки, при котором совокупность всех участников, соответствующих критериям включения в исследование, сначала разделяется на группы (страты) на основе одной или нескольких характеристик (обычно пола, возраста), потенциально влияющих на изучаемый исход, а затем из каждой из этих групп (страт) независимо проводится набор участников в экспериментальную и контрольную группы. Это позволяет исследователю соблюдать баланс важных характеристик между экспериментальной и контрольной группами.
Таблица сопряженности
Определение. Таблица абсолютных частот (количества) наблюдений, столбцы которой соответствуют значениям одного признака, а строки - значениям другого признака (в случае двумерной таблицы сопряженности). Значения абсолютных частот располагаются в клетках на пересечении рядов и колонок.
Приведем пример таблицы сопряженности. Операция на аневризме была сделана 194 пациентам. Известен показатель выраженности отека у пациентов перед операцией.
|
Отек\ Исход | |||
|---|---|---|---|
| нет отека | 20 | 6 | 26 |
| умеренный отек | 27 | 15 | 42 |
| выраженный отек | 8 | 21 | 29 |
| m j | 55 | 42 | 194 |
Таким образом, из 26 пациентов, не имеющих отека, после операции выжило 20 пациентов, умерло - 6 пациентов. Из 42 пациентов, имеющих умеренный отек выжило 27 пациентов, умерло - 15 и т.д.
Критерий хи-квадрат для таблиц сопряженности
Для определения значимости (достоверности) различий одного признака в зависимости от другого (например, исхода операции в зависимости от выраженности отека) применяется критерий хи-квадрат для таблиц сопряженности:
Шанс
Пусть вероятность некоторого события равна p. Тогда вероятность того, что событие не произойдёт равна 1-p.
Например, если вероятность того, что больной останется жив спустя пять лет равна 0.8 (80%), то вероятность того, что он за этот временной промежуток умрёт равна 0.2 (20%).
Определение. Шанс - это отношение вероятности того, что события произойдёт к вероятности того, что событие не произойдёт.
Пример. В нашем примере (про больного) шанс равен 4, так как 0.8/0.2=4
Таким образом, вероятность выздоровления в 4 раза больше вероятности смерти.
Интерпретация значения величины.
1) Если Шанс=1, то вероятность наступления события равна вероятности того, что событие не произойдёт;
2) если Шанс >1, то вероятность наступления события больше вероятности того, что событие не произойдёт;
3) если Шанс <1, то вероятность наступления события меньше вероятности того, что событие не произойдёт.
Отношение шансов
Определение. Отношение шансов (odds ratio) - это отношение шансов для первой группы объектов к отношению шансов для второй группы объектов.
Пример. Допустим, что некоторое лечение проходят и мужчины, и женщины.
Вероятность того, что больной мужского пола останется жив спустя пять лет равна 0.6 (60%); вероятность того, что он за этот временной промежуток умрёт равна 0.4 (40%).
Аналогичные вероятности для женщин равны 0.8 и 0.2.
Отношение шансов в этом примере равно
Интерпретация значения величины.
1) Если отношение шансов =1, то шанс для первой группы равен шансу для второй группы
2) Если отношение шансов >1, то шанс для первой группы больше шанса для второй группы
3) Если отношение шансов <1, то шанс для первой группы меньше шанса для второй группы
Совсем недавно Владимир Давыдов написал пост в facebook про A/B- или MVT-тестирование, который вызвал массу вопросов.
Обычно проведение A/B- или MVT-тестирований на сайтах — вещь очень сложная. Хотя «посадочникам» кажется, что это элементарно, ведь «этсамое, есть же специальные программы, гыг».
Если вы решили тестировать веб-содержимое, помните:
1. Для начала нужно изолировать равнозначную, равновеликую, равнокачественную аудиторию. Провести A/A-тесты. Подавляющее большинство тестов, которые проводят агентства на потоке или неопытные интернет-маркетологи, не верны. Именно по той причине, что тестируется содержимое на разных аудиториях.
2. Проводите десятки или лучше сотни тестов в течение нескольких месяцев. Тестировать недельку 2-3 варианта странички не стоит.
3. Помните, что тестировать можно и в формате MVT (то есть много вариантов), а не только A и B.
4. Статистически проанализируйте массив данных с результатами тестов (в Excel абсолютно окей, можно ещё SPSS использовать). Находятся ли результаты в рамках погрешности, насколько сильно отклоняются и как зависят от времени. Если, например, в первом пункте A/A-теста вы получили сильные отклонения одного варианта от другого — это провал, и дальше тестировать нельзя.
5. Не надо тестировать все подряд. Это не развлечение (только если вам реально больше нечего делать). Тестировать имеет смысл только то, что с точки зрения маркетингового и бизнес-анализа способно привести к заметным результатам. А также то, результат от чего можно реально измерить. Например, вы решили увеличить размер шрифта на сайте, потестировали пару недель страницу с большим шрифтом — продажи выросли. О чем это говорит? Вот и мне ни о чем (см. предыдущие пункты).
6. Тестировать нужно пути целиком. То есть недостаточно взять и протестировать страницу покупки (или какого-то действия на сайте) — нужно тестировать и те страницы и шаги, которые подводят к этой финальной конверсионной странице.
В комментариях был задан вопрос:
«Как устанавливать победителя? Вот протестировали мы заголовок на странице, продающей «в лоб». Какая разница в конверсии должна быть между А и B, чтобы признать победителя?»
Ответ Владимира:
Во-первых, нужно проводить длительные изолированные эксперименты (базовое правило любой статистической оценки). Во-вторых, все неминуемо сводится к статистике и математике (поэтому и рекомендую excel и spss или аналоги бесплатные) Нам нужно посчитать доверительную вероятность того, что разница в значениях чего-то значит. Есть хорошая статья (одна из многих). Там берут транзакции из GA по проводимым Optimizely-тестам https://www.distilled.net/uploads/ga_transactions.png , сравнивают транзакции (покупки) обычным колокольным распределением и смотрят, попадает ли среднее значение в рамки доверительного интервала погрешности https://www.distilled.net/uploads/t-test_tool.png
Хотите получить предложение от нас?
Начать сотрудничествоРоль статистической значимости при повышении конверсии: 6 вещей, которые нужно знать
1. Именно то, что это значит

«Изменение позволило достичь повышения конверсии на 20% с доверительной вероятностью 90%». К сожалению, это утверждение вовсе не равнозначно другому, очень похожему: «Шансы повысить конверсию на 20% составляют 90%». Так о чем же речь на самом деле?
20% — это рост, который мы зафиксировали по результатам тестов на одном из образцов. Если бы мы начали фантазировать и строить догадки, мы бы могли предположить, что этот рост может сохраняться постоянно – если мы будем продолжать тестирование до бесконечности. Но это никак не означает, что с вероятностью 90% мы получим двадцатипроцентный рост конверсии или рост «как минимум» в 20%, или «приблизительно» в 20%.
90% — это вероятность проявления каких бы то ни было изменений в конверсии. Другими словами, если бы мы проводили десять А/B-тестов, чтобы получить этот результат, и решили бы проводить все десять до бесконечности, то один из них (так как вероятность изменений 90%, то 10% остаётся на неизменный исход), вероятно, закончился бы приближением результата «после теста» к первоначальной конверсии – то есть, без изменений. Из остающихся девяти тестов некоторые могли бы показать рост, составляющий куда меньше 20%. В других результат мог бы превысить эту планку.
Если неверно интерпретировать эти данные, мы сильно рискуем, «выкатывая» тест. Легко обрадоваться, когда тест показывает высокие показатели роста конверсии с доверительной вероятностью в 95%, но мудрее было бы не ожидать слишком многого, пока тест не доведен до логического завершения.
2. Когда использовать
Самые очевидные кандидаты – сплит-тесты «А/В», но они далеко не единственные. Можно также проводить тестирование статистически значимой разницы между сегментами (например, посещениями через обычный и через оплаченный поиск) или временными промежутками (например, апрелем 2013 года и апрелем 2014 года).
Однако стоит заметить, что эта корреляция не подразумевает причинно-следственную связь. Проводя сплит-тесты, мы знаем, что можем приписать любые изменения результатов тем элементам, которыми различаются страницы – ведь особое внимание уделяется тому, чтобы в остальном страницы были совершенно идентичны. Если вы сравниваете такие группы, как посетители, пришедшие из обычного и платного поиска, сработать могут любые другие факторы – к примеру, из обычного поиска может быть много посещений по ночам, а конверсия среди ночных посетителей весьма высока. Тесты на значимость помогают установить, есть ли у изменений причина, но они не смогут сказать, в чем именно она заключается.
3. Как тестировать изменения показателей конверсии, отказов и выходов (exit rate)
Когда мы смотрим на «показатели», на самом деле мы видим усредненные значения двоичных переменных – кто-то либо выполнил целевые действия, либо нет. Если у нас есть выборка в 10 человек с показателем конверсии в 40%, на самом деле мы смотрим на подобную таблицу:

Эта таблица потребуется нам вкупе со средним показателем, чтобы вычислить среднее отклонение – ключевой компонент статистической значимости. Однако тот факт, что каждое значение в таблице является либо нулем, либо единицей, облегчает нам задачу – мы можем обойтись без необходимости копировать огромный список цифр, воспользовавшись калькулятором для подсчета доверительной вероятности А/B-тестов, и отталкиваясь от знания среднего показателя и размеров выборки. Это инструмент от KissMetrics .

(Важно! Этот инструмент в расчетах принимает во внимание только одну сторону “колокола” распределения вероятности . Чтобы использовать обе стороны и перевести результат в двустороннюю значимость, нужно удвоить дистанцию от 100% — например, односторонние 95% становятся двусторонними 90%).
Несмотря на то, что в описании значится «инструмент тестирования достоверности А/B-тестов», его также можно использовать для любого другого сравнения показателей – просто замените конверсию на показатель отказов или выходов. Кроме того, его можно использовать и для сравнения сегментов или промежутков времени – вычисления будут те же.
Также, он хорошо подходит для мультивариантных тестирований (MVT) – просто сравнивайте с оригиналом каждое изменение по отдельности.
4. Как тестировать изменения среднего чека
Чтобы тестировать средние значение недвоичных переменных, нам потребуется полный набор данных, так что здесь все немного сложнее. Например, мы хотим установить, есть ли значимые различия средней суммы заказа для сплит-теста А/В – этот момент часто опускают при оптимизации конверсии, хотя для бизнес-показателей он так же важен, как и сама конверсия.
Первое, что нам нужно, это получить из Google Analytics полный список транзакций для каждого варианта теста — для А и B (было, стало). Простейший способ это сделать – создать пользовательские сегменты, базирующиеся на переменных (custom variables) для вашего сплит-теста, а затем экспортировать отчет по транзакциям в таблицу Excel. Убедитесь, что туда войдут все транзакции, а не только 10 строк, указанных по умолчанию.

Когда у вас есть два списка транзакций, их можно скопировать в подобный инструмент :
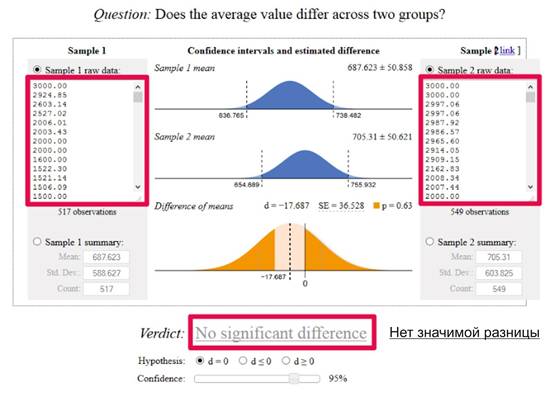
В вышеозначенном случае у нас нет доверительной вероятности на выбранном уровне в 95%. На самом деле, если мы взглянем на показатель «p» над нижним графиком, составляющий 0,63, станет ясно, что у нас нет даже 50% значимости – существует вероятность в 63%, что разница между показателями страниц является чистой случайностью.
5. Как предугадать необходимую продолжительность сплит-теста А/В
На Evanmiller.org есть еще один удобный инструмент для оптимизации конверсии – калькулятор размера выборки .
Этот инструмент позволяет дать ответ на вопрос «Сколько потребуется времени, чтобы получить достоверные результаты теста?», и этот ответ не стоит пытаться угадать.

Стоит отметить несколько моментов. Во-первых, у инструмента есть переключатель «абсолютное/относительное» — если вы хотите выяснить разницу между базовым показателем конверсии в 5% и переменным показателем конверсии в 6%, он составит 1% в абсолютном выражении (6-5=1) или 20% в относительном выражении (6/5=1,2). Во-вторых, внизу страницы есть два «бегунка». Нижний отвечает за требуемый уровень значимости – если вашей целью является получение значимости в 95%, то бегунок нужно выставить на 5%. Верхний бегунок показывает вероятность того, что количество требуемых посещений страницы окажется достаточным – к примеру, если вы хотите узнать количество визитов, необходимых для достижения восьмидесяти процентного шанса обнаружить значимость в 95%, выставьте верхний бегунок на 80%, а нижний на 5%.
6. Чего не нужно делать
Есть несколько простых путей выявить непригодность сплит-теста, которые, однако, далеко не всегда очевидны с первого взгляда:
А) Сплит-тестирование недвоичных порядковых значений
Например, ваша цель – выяснить, имеет ли место значимая разница вероятностей того, что посетители из групп «первоначальная» и «после изменений» купят определенные продукты. Вы помечаете три продукта «1», «2» и «3», а затем вводите эти значения в поля теста на значимость. К сожалению, этот подход не сработает – продукт 2 не является средним значением продуктов 1 и 3.
Б) Настройки распределения трафика

В начале теста вы решаете не рисковать и выставляете распределение трафика 90/10. Спустя какое-то время вы видите, что изменение не привело к заметным изменениям в конверсии, и перемещаете бегунок к значению 50/50. Но возвращающиеся посетители по-прежнему принадлежат к своей первоначальной группе, поэтому вы оказываетесь в ситуации, где версия «до изменений» отличается большей долей вернувшихся посетителей, показывающих высокую вероятность конверсии. Все очень быстро усложняется, и единственный простой путь получить данные, на которые можно положиться, заключается в том, чтобы по отдельности рассматривать новых и вернувшихся посетителей. Однако в этом случае на получение значимых результатов уйдет больше времени. И даже если обе подгруппы покажут значимые результаты, что, если одна из них на самом деле генерирует больше вернувшихся посетителей? В общем, не нужно этого делать и менять в течение теста распределение трафика.
В) Планирование
Выглядит очевидным, но не стоит сравнивать данные, собранные в одно и то же время дня, с данными, собранными в течение суток или в другое время дня. Если вы хотите провести тест в отношении конкретного времени дня, у вас есть два варианта.
1. Обрабатывать запросы посетителей, как и всегда, в течение дня, но показывать им оригинальную версию страницы в то время дня, в котором вы не заинтересованы.
2. Сравнивать яблоки с яблоками – если вы рассматриваете только данные по изменениям за первую половину дня, сравнивайте их с первоначальными данными за первую половину дня.
Надеюсь, что-то из вышеизложенного окажется полезным для оптимизации вашей конверсии . Если у вас есть свои ноу-хау, пожалуйста, излагайте их в комментариях.
Как вы думаете, что делает вашу «вторую половинку» особенной, значимой? Это связано с ее (его) личностью или с вашими чувствами, которые вы испытываете к этому человеку? А может, с простым фактом, что гипотеза о случайности вашей симпатии, как показывают исследования, имеет вероятность менее 5%? Если считать последнее утверждение достоверным, то успешных сайтов знакомств не существовало бы в принципе:
Когда вы проводите сплит-тестирование или любой другой анализ вашего сайта, неверное понимание «статистической значимости» может привести к неправильной интерпретации результатов и, следовательно, ошибочным действиям в процессе оптимизации конверсии. Это справедливо и для тысяч других статистических тестов, проводимых ежедневно в любой существующей отрасли.
Чтобы разобраться, что же такое «статистическая значимость», необходимо погрузиться в историю появления этого термина, познать его истинный смысл и понять, как это «новое» старое понимание поможет вам верно трактовать результаты своих исследований.
Немного истории
Хотя человечество использует статистику для решения тех или иных задач уже много веков, современное понимание статистической значимости, проверки гипотез, рандомизации и даже дизайна экспериментов (Design of Experiments (DOE) начало формироваться только в начале 20-го столетия и неразрывно связано с именем сэра Рональда Фишера (Sir Ronald Fisher, 1890-1962):

Рональд Фишер был эволюционным биологом и статистиком, который имел особую страсть к изучению эволюции и естественного отбора в животном и растительном мире. В течение своей прославленной карьеры он разработал и популяризировал множество полезных статистических инструментов, которыми мы пользуемся до сих пор.
Фишер использовал разработанные им методики, чтобы объяснить такие процессы в биологии, как доминирование, мутации и генетические отклонения. Те же инструменты мы можем применить сегодня для оптимизации и улучшения контента веб-ресурсов. Тот факт, что эти средства анализа могут быть задействованы для работы с предметами, которых на момент их создания даже не существовало, кажется довольно удивительным. Столь же удивительно, что раньше сложнейшие вычисления люди выполняли без калькуляторов или компьютеров.
Для описания результатов статистического эксперимента как имеющих высокую вероятность оказаться истиной Фишер использовал слово «значимость» (от англ. significance).
Также одной из наиболее интересных разработок Фишера можно назвать гипотезу «сексуального сына». Согласно этой теории, женщины отдают свое предпочтение неразборчивым в половых связях мужчинам (гулящим), потому что это позволит рожденным от этих мужчин сыновьям иметь такую же предрасположенность и произвести на свет больше своих отпрысков (обращаем внимание, что это всего лишь теория).
Но никто, даже гениальные ученые, не застрахованы от совершения ошибок. Огрехи Фишера досаждают специалистам и по сей день. Но помните слова Альберта Эйнштейна: «Кто никогда не ошибался, тот не создавал ничего нового».
Прежде чем перейти к следующему пункту, запомните: статистическая значимость — это ситуация, когда разница в результатах при проведении тестирования настолько велика, что эту разницу нельзя объяснить влиянием случайных факторов.
Какова ваша гипотеза?
Чтобы понять, что значит «статистическая значимость», сначала нужно разобраться с тем, что такое «проверка гипотез», поскольку два этих термина тесно переплетаются.
Гипотеза — это всего лишь теория. Как только вы разработаете какую-либо теорию, вам будет необходимо установить порядок сбора достаточного количества доказательств и, собственно, собрать эти доказательства. Существует два типа гипотез.

Яблоки или апельсины — что лучше?
Нулевая гипотеза
Как правило, именно в этом месте многие испытывают трудности. Нужно иметь в виду, что нулевая гипотеза — это не то, что нужно доказать, как, например, вы доказываете, что определенное изменение на сайте приведет к повышению конверсии, а наоборот. Нулевая гипотеза — это теория, которая гласит, что при внесении каких-либо изменений на сайт ничего не произойдет. И цель исследователя — опровергнуть эту теорию, а не доказать.
Если обратиться к опыту раскрытия преступлений, где следователи также строят гипотезы в отношении того, кто является преступником, нулевая гипотеза принимает вид так называемой презумпции невиновности, концепта, согласно которому обвиняемый считается невиновным до тех пор, пока его вина не будет доказана в суде.
Если нулевая гипотеза заключается в том, что два объекта равны в своих свойствах, а вы пытаетесь доказать, что один из них все же лучше (например, A лучше B), вам нужно отказаться от нулевой гипотезы в пользу альтернативной. Например, вы сравниваете между собой тот или иной инструмент для оптимизации конверсии. В нулевой гипотезе они оба оказывают на объект воздействия одинаковый эффект (или не оказывают никакого эффекта). В альтернативной — эффект от одного из них лучше.
Ваша альтернативная гипотеза может содержать числовое значение, например, B - A > 20%. В таком случае нулевая гипотеза и альтернативная могут принять следующий вид:

Другое название для альтернативной гипотезы — это исследовательская гипотеза, поскольку исследователь всегда заинтересован в доказательстве именно этой гипотезы.
Статистическая значимость и значение «p»
Вновь вернемся к Рональду Фишеру и его понятию о статистической значимости.
Теперь, когда у вас есть нулевая гипотеза и альтернативная, как вы можете доказать одно и опровергнуть другое?
Поскольку статистические данные по самой своей природе предполагают изучение определенной совокупности (выборки), вы никогда не можете быть на 100% уверены в полученных результатах. Наглядный пример: зачастую результаты выборов расходятся с результатами предварительных опросов и даже эксит-пулов.
Доктор Фишер хотел создать определитель (dividing line), который позволял бы понять, удался ли ваш эксперимент или нет. Так и появился индекс достоверности. Достоверность — это тот уровень, который мы принимаем для того, чтобы сказать, что мы считаем «значимым», а что нет. Если «p», индекс достоверности, равен 0,05 или меньше, то результаты достоверны.
Не волнуйтесь, в действительности все не так запутано, как кажется.

Распределение вероятностей Гаусса. По краям — менее вероятные значения переменной, в центре — наиболее вероятные. P-показатель (закрашенная зеленым область) — это вероятность наблюдаемого результата, возникающего случайно.
Нормальное распределение вероятностей (распределение Гаусса) — это представление всех возможных значений некой переменной на графике (на рисунке выше) и их частот. Если вы проведете свое исследование правильно, а затем расположите все полученные ответы на графике, вы получите именно такое распределение. Согласно нормальному распределению, вы получите большой процент похожих ответов, а оставшиеся варианты разместятся по краям графика (так называемые «хвосты»). Такое распределение величин часто встречается в природе, поэтому оно и носит название «нормального».
Используя уравнение на основе вашей выборки и результатов теста, вы можете вычислить то, что называется «тестовой статистикой», которая укажет, насколько отклонились полученные результаты. Она также подскажет, насколько близко вы к тому, чтобы нулевая гипотеза оказалась верной.
Чтобы не забивать свою голову, используйте онлайн-калькуляторы для вычисления статистической значимости:

Один из примеров таких калькуляторов
Буква «p» обозначает вероятность того, что нулевая гипотеза верна. Если число будет небольшим, это укажет на разницу между тестовыми группами, тогда как нулевая гипотеза будет заключаться в том, что они одинаковы. Графически это будет выглядеть так, что ваша тестовая статистика окажется ближе к одному из хвостов вашего колоколообразного распределения.
Доктор Фишер решил установить порог достоверности результатов на уровне p ≤ 0,05. Однако и это утверждение спорное, поскольку приводит к двум затруднениям:
1. Во-первых, тот факт, что вы доказали несостоятельность нулевой гипотезы, не означает, что вы доказали альтернативную гипотезу. Вся эта значимость всего лишь значит, что вы не можете доказать ни A, ни B.
2. Во-вторых, если p-показатель будет равен 0,049, это будет означать, что вероятность нулевой гипотезы составит 4,9%. Это может означать, что в одно и то же время результаты ваших тестов могут быть одновременно и достоверными, и ошибочными.
Вы можете использовать p-показатель, а можете отказаться от него, но тогда вам будет необходимо в каждом отдельном случае высчитывать вероятность осуществления нулевой гипотезы и решать, достаточно ли она большая, чтобы не вносить тех изменений, которые вы планировали и тестировали.
Наиболее распространенный сценарий проведения статистического теста сегодня — это установление порога значимости p ≤ 0,05 до запуска самого теста. Только не забудьте внимательно изучить p-значение при проверке результатов.
Ошибки 1 и 2
Прошло так много времени, что ошибки, которые могут возникнуть при использовании показателя статистической значимости, даже получили собственные имена.
Ошибка 1 (Type 1 Errors)
Как было упомянуто выше, p-значение, равное 0,05, означает: вероятность того, что нулевая гипотеза окажется верной, равняется 5%. Если вы откажетесь от нее, вы совершите ошибку под номером 1. Результаты говорят, что ваш новый веб-сайт повысил показатели конверсии, но существует 5%-ная вероятность, что это не так.
Ошибка 2 (Type 2 Errors)
Эта ошибка является противоположной ошибке 1: вы принимаете нулевую гипотезу, в то время как она является ложной. К примеру, результаты тестов говорят вам, что внесенные изменения в сайт не принесли никаких улучшений, тогда как изменения были. Как итог: вы упускаете возможность повысить свои показатели.
Такая ошибка распространена в тестах с недостаточным размером выборки, поэтому помните: чем больше выборка, тем достовернее результат.
Заключение
Пожалуй, ни один термин среди исследователей не пользуется такой популярностью, как статистическая значимость. Когда результаты тестов не признаются статистически значимыми, последствия бывают самые разные: от роста показателя конверсии до краха компании.
И раз уж маркетологи используют этот термин при оптимизации своих ресурсов, нужно знать, что же он означает на самом деле. Условия проведения тестов могут меняться, но размер выборки и критерий успеха важен всегда. Помните об этом.
Основные черты всякой зависимости между переменными.
Можно отметить два самых простых свойства зависимости между переменными: (a) величина зависимости и (b) надежность зависимости.
- Величина . Величину зависимости легче понять и измерить, чем надежность. Например, если любой мужчина в выборке имел значение числа лейкоцитов (WCC) выше чем любая женщина, то вы можете сказать, что зависимость между двумя переменными (Пол и WCC) очень высокая. Другими словами, вы могли бы предсказать значения одной переменной по значениям другой.
- Надежность ("истинность"). Надежность взаимозависимости - менее наглядное понятие, чем величина зависимости, однако чрезвычайно важное. Надежность зависимости непосредственно связана с репрезентативностью определенной выборки, на основе которой строятся выводы. Другими словами, надежность говорит о том, насколько вероятно, что зависимость будет вновь обнаружена (иными словами, подтвердится) на данных другой выборки, извлеченной из той же самой популяции.
Следует помнить, что конечной целью почти никогда не является изучение данной конкретной выборки значений; выборка представляет интерес лишь постольку, поскольку она дает информацию обо всей популяции. Если исследование удовлетворяет некоторым специальным критериям, то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры.
Величина зависимости и надежность представляют две различные характеристики зависимостей между переменными. Тем не менее, нельзя сказать, что они совершенно независимы. Чем больше величина зависимости (связи) между переменными в выборке обычного объема, тем более она надежна (см. следующий раздел).
Статистическая значимость результата (p-уровень) представляет собой оцененную меру уверенности в его "истинности" (в смысле "репрезентативности выборки"). Выражаясь более технически, p-уровень – это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий p-уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно, p-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию.
Например, p-уровень = 0.05 (т.е. 1/20) показывает, что имеется 5% вероятность, что найденная в выборке связь между переменными является лишь случайной особенностью данной выборки. Во многих исследованиях p-уровень 0.05 рассматривается как "приемлемая граница" уровня ошибки.
Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать "значимым". Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, является достаточно произвольным.
На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т.е. до проведения опыта) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований.
Обычно во многих областях результат p .05 является приемлемой границей статистической значимости, однако следует помнить, что этот уровень все еще включает довольно большую вероятность ошибки (5%).
Результаты, значимые на уровне p .01 обычно рассматриваются как статистически значимые, а результаты с уровнем p .005 или p . 001 как высоко значимые. Однако следует понимать, что данная классификация уровней значимости достаточно произвольна и является всего лишь неформальным соглашением, принятым на основе практического опыта в той или иной области исследования .
Понятно, что чем большее число анализов будет проведено с совокупностью собранных данных, тем большее число значимых (на выбранном уровне) результатов будет обнаружено чисто случайно.
Некоторые статистические методы, включающие много сравнений, и, таким образом, имеющие значительный шанс повторить такого рода ошибки, производят специальную корректировку или поправку на общее число сравнений. Тем не менее, многие статистические методы (особенно простые методы разведочного анализа данных) не предлагают какого-либо способа решения данной проблемы.
Если связь между переменными "объективно" слабая, то не существует иного способа проверить такую зависимость кроме как исследовать выборку большого объема. Даже если выборка совершенно репрезентативна, эффект не будет статистически значимым, если выборка мала. Аналогично, если зависимость "объективно" очень сильная, тогда она может быть обнаружена с высокой степенью значимости даже на очень маленькой выборке.
Чем слабее зависимость между переменными, тем большего объема требуется выборка, чтобы значимо ее обнаружить.
Разработано много различных мер взаимосвязи между переменными. Выбор определенной меры в конкретном исследовании зависит от числа переменных, используемых шкал измерения, природы зависимостей и т.д.
Большинство этих мер, тем не менее, подчиняются общему принципу: они пытаются оценить наблюдаемую зависимость, сравнивая ее с "максимальной мыслимой зависимостью" между рассматриваемыми переменными. Говоря технически, обычный способ выполнить такие оценки заключается в том, чтобы посмотреть, как варьируются значения переменных и затем подсчитать, какую часть всей имеющейся вариации можно объяснить наличием "общей" ("совместной") вариации двух (или более) переменных.
Значимость зависит в основном от объема выборки. Как уже объяснялось, в очень больших выборках даже очень слабые зависимости между переменными будут значимыми, в то время как в малых выборках даже очень сильные зависимости не являются надежными.
Таким образом, для того чтобы определить уровень статистической значимости, нужна функция, которая представляла бы зависимость между "величиной" и "значимостью" зависимости между переменными для каждого объема выборки.
Такая функция указала бы точно "насколько вероятно получить зависимость данной величины (или больше) в выборке данного объема, в предположении, что в популяции такой зависимости нет". Другими словами, эта функция давала бы уровень значимости
(p -уровень), и, следовательно, вероятность ошибочно отклонить предположение об отсутствии данной зависимости в популяции.
Эта "альтернативная" гипотеза (состоящая в том, что нет зависимости в популяции) обычно называется нулевой гипотезой .
Было бы идеально, если бы функция, вычисляющая вероятность ошибки, была линейной и имела только различные наклоны для разных объемов выборки. К сожалению, эта функция существенно более сложная и не всегда точно одна и та же. Тем не менее, в большинстве случаев ее форма известна, и ее можно использовать для определения уровней значимости при исследовании выборок заданного размера. Большинство этих функций связано с классом распределений, называемым нормальным .

 Вход
Вход